路漫漫其修远兮 吾将上下而求索
0%

深度学习-5day

发表于 分类于

张量的存储视图

在底层代码种，张量中的被分配到由torch.storage实例所管理的连续内存块当中，存储区是由数字数据所组成的一维数组，即包含给定类型的数字的连续内存块，如下图所示

1
2
3
4
5
6
7
----------------|   张量(引用相同的储存区)   |-----------------|
| 4 | 1 | 5 |                              |  4  |  1  |
| 3 | 2 | 1 |                              |  5  |  3  |
从0开始，2行3列                             |  2  |  1  |
                                           从0开始，3行2列
存储区| 4 | 1 | 5 | 3 | 2 | 1 |.................
                    张量是storage实例视图

索引储存区

在实际中如何使用二位点来索引储存区，可以使用storage()访问给定张量的存储区：

1
2
3
4
5
6
points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]]) points.storage() 

输出
<bound method Tensor.storage of tensor([[1., 2.],
        [2., 3.],
        [3., 4.]])>

在底层中，事实上储存的是一个连续的大小为6的连续数组，但是在你打印的时候是会自动进行还原的，我们可以手动索引储存区

1
2
3
4
5
a = torch.tensor([[1,2],[2,3],[3,4]],dtype=torch.float32)
b = a.storage()
print(b[0])
输出
1.0

不能使用两个索引来索引二维张量的存储区，不管和存储区相关的任何其他张量的维度是多少，他的布局始终都是一维，也可以通过索引直接改变存储区的值

张量元数据

为了在存储区中建立索引，张量依赖于一些明确定义他们的信息，大小，偏移量和步长，大小，在numpy中又被称之为形状是一个元组，表示张量在每一个维度上有多少元素，偏移量就是指存储区中某元素相对第一个元素的索引，步长是指存储区中为了获得下一个元素需要跳过的元素的数量

图片

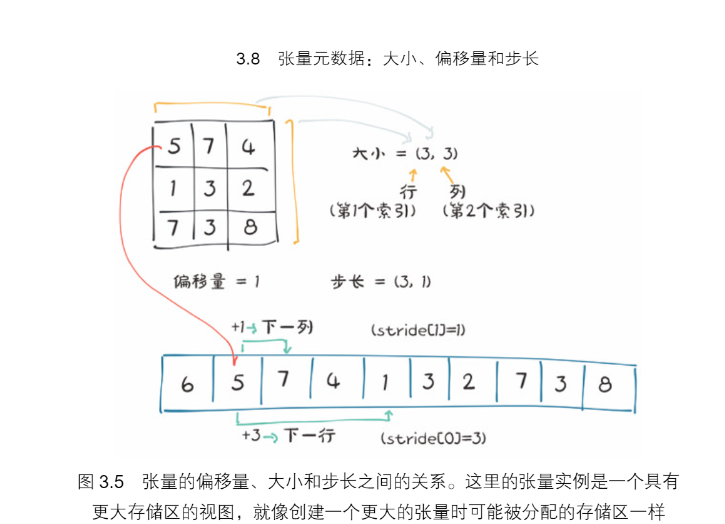
另一个张量的存储视图

我们可以通过提供相应的索引来得到张量中的第二个点，

1
2
points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]]) second_point = points[1] 
second_point.storage_offset()//返回相对第一个元素的位置的偏移量

函数size和shape属性所包含的信息是一致的

1
2
3
second_point.shape

torch.Size([2])

步长是一个元素，知识当索引在每一个维度增加1的时候在存储区中必须要跳过的元素的数量，

1
2
3
例如points的步长为（2，1），意思就是
- 第一个数字 2 ：表示在第0维（行）上移动一格时，需要在底层存储中跳过2个元素。
- 第二个数字 1 ：表示在第1维（列）上移动一格时，需要跳过1个元素。

使用stride方法就可以获取到步长

当我们索引一个特定的点，同时看到偏移量增加，表名我们已经提取了一个子张量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
second_point = points[1] 
second_point.size()

输出
torch.Size([2])

second_point.storage_offset()#

输出
2

second_point.stride()

输出
(1,)

正如预期的那样，子张量的维度少了一维，但仍然能索引到与原始张量相同的存储区，更改子张量也会对原始张量产生影响

1
2
3
4
5
6
7
points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]]) second_point = points[1] 
second_point[0] = 10.0 points 

输出
tensor([[ 4., 1.],         
		[10., 3.],         
		[ 2., 1.]])

可以使用clone方法将这个子张量复制成一个新的张量

1
2
3
4
5
6
7
8
points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]]) second_point = points[1].clone() 
second_point[0] = 10.0 
points 

输出
tensor([[4., 1.],        
	[5., 3.],         
	[2., 1.]]
无复制转置

使用张量points，它在行中有单独的点，在列中有x和y的坐标，然后将其转置，使各个点都在列中，使用t()方法，用于转置一个矩阵

并且这样转置出来的矩阵和原矩阵共用一个存储区

1
2
3
4
5
6
7
8
9
10
11
12
points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]]) 
second_point = points[1].clone() 
print(points.t())

输出
tensor([[4., 5., 2.],
        [1., 3., 1.]])
        
可以验证这两个张量共享一个存储区
id(points.storage()) == id(points_t.storage())
输出
true

只是在形状和步长上有所不同

将张量转置之后，如下图所示，我们在步长中改变元素顺序之后，增加的行将沿着存储区跳跃一个单位，就像沿着原张量的列移动一样，转置不会分配新的内存只是创建一个tensor的实例

图片

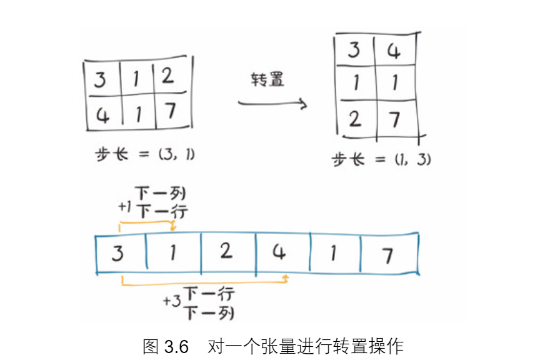
连续张量

在pytorch中一些张量操作只对连续的张量起作用，使用contifuous方法可以将一个不连续的张量转换成一个连续的张量，但是步长和存储发生了改变

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
points = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]]) 、points_t = points.t() #转置
points_t 

输出
tensor([[4., 5., 2.],         
	[1., 3., 1.]])
	
points_t.storage()
输出
4.0   1.0   5.0   3.0   2.0   1.0#存储区域

points_t.stride()#计算步长

输出
(1,2)

points_t_cont = points_t_cont.contiguous()#转换
points_t_cont

输出
tensor([[4., 5., 2.],         
		[1., 3., 1.]])#可以看到已经发生了转置
		
points_t_cont.stride()#计算步长

输出
(3,1)#可以看到步长已经发生了改变

points_t_cont.storage()

输出
4.0   5.0   2.0   1.0   3.0   1.0#存储区也发生了变化

将张量存储到Gpu

pytorch最重要的能够大幅提升运行速度的特性就是可以在gpu上和cpu上同时与逆行，以大规模的提升运算速度

管理张量的设备属性

pytorch张量还有device的概念，就是张量数据在计算机上的位置

1
points_gpu = torch.tensor([[4.0, 1.0], [5.0, 3.0], [2.0, 1.0]], device='cuda')

可以使用to方法将在cpu上创建的张量复制到gpu上：

1
points_gpu = points.to(device='cuda')

这样将会返回一个新的张量

序列化张量

创建动态的张量是很好的，但是如果里面的数据是有价值的，我们希望将其保存到一个文件当中，可以免去每次运行程序的时候都要从头开始对模型进行训练，可以使用pickle来序列化张量对象，并为存储添加专用的序列化代码，

1
torch.save(points, '../data/p1ch3/ourpoints.t')

加载张量同样可以通过一行代码来实现

1
points = torch.load('../data/p1ch3/ourpoints.t')

用这种方法可以快速的保存张量和使用张量