深度学习-8day

表示表格数据

使用独热编码

另一种方法是构建分数的一个独热编码，就是将10个分数分别编码到一个由10个元素组成的向量中，除了其中一个元素设置为1，其他的元素都设置为0，它的主要作用包括：

1. 处理分类数据 ：将分类特征（如颜色、品牌等）转换为数值形式，使机器学习算法能够处理。
2. 避免序数关系 ：防止算法错误地解释类别之间存在大小关系。例如，如果将”红、绿、蓝”编码为1、2、3，算法可能会误认为蓝色(3)比红色(1)更重要。
3. 增加特征维度 ：每个类别变成一个二进制特征，使模型能够学习到每个类别的独立影响。
4. 提高模型表达能力 ：特别是对于树模型以外的算法（如线性回归、神经网络等），独热编码可以帮助模型更好地学习非线性关系。

如果分数是完全离散的，比如葡萄酒的品种，那么采用独热编码更为合适，因为没有隐含的顺序和距离，独热编码也适用于分数介于整数分数之间的定量分数

我们可以使用scatter_()方法获得一个独热编码，该方法将沿着参数提供的索引方向，将源张量的值填充大输入张量中

target_onebot = torch.zeros(target.shape[0],10)

target_onehot.scatter_(1,target.unsequeeze(1),1.0)
这里需要保证target是一个一维向量，我们可以选择数据集的最后一列，然后通过unsequeeze方法扩充维度
#关于scatter_()函数的参数
指定以下2个参数的维度。
一个列张量，表示要散射的元素的索引张量。
包含要散射的元素的张量，或要散射的单个标量（在这种情况下为1.0）

如果我们想将分数作为网络的分类输入，就必须将它转化为一个独热编码张量

何时分类

现在已经知道了处理连续数据和分类数据的方法，但是前面有序数据是如何处理的呢，处理这些数据没有通用的方法，最常见的是将这些数据视为分类数据或者连续数据

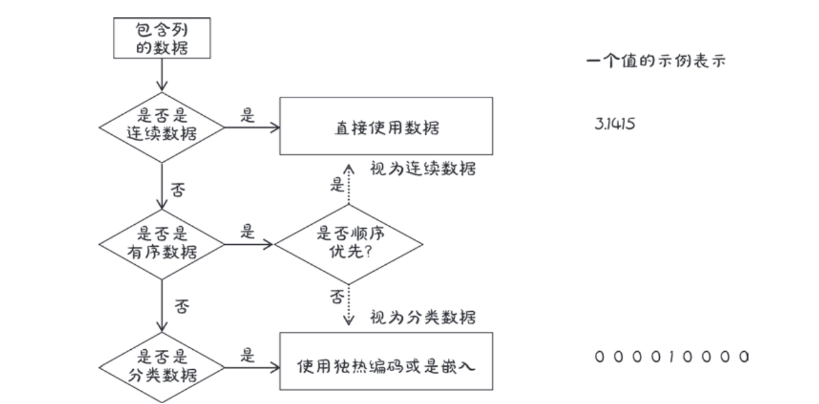
回到张量data，它包含与化学特征分析相关的11个变量，我们可以使用pytorch张量api中的函数来处理张量表格数据，让我们首先获得每一列的平均值和标准差

data_mean = torch.mean(data, dim=0)
#- 计算 data 张量沿着维度0（行维度）的平均值
- 这意味着对每一列的所有数值求平均，得到每个特征的平均值
print(data_mean)

输出
tensor([8.0000e+02, 8.3196e+00, 5.2782e-01, 2.7098e-01, 2.5388e+00, 8.7467e-02,
        1.5875e+01, 4.6468e+01, 9.9675e-01, 3.3111e+00, 6.5815e-01, 1.0423e+01])

获取方差
data_var = torch.var(data, dim=0)
#- 这行代码计算了 data 张量沿着维度0（行维度）的方差
- torch.var() 是PyTorch中计算方差的函数
- dim=0 参数指定沿着第一个维度（行）计算方差
- 方差是衡量数据分散程度的统计量，它表示数据点与平均值之间差异的平方的平均值
- 对于每个特征（列），这个函数计算所有样本在该特征上的方差
- 结果是一个一维张量，包含每个特征的方差值
print(data_var)

输出
tensor([2.1320e+05, 3.0314e+00, 3.2062e-02, 3.7947e-02, 1.9879e+00, 2.2151e-03,
        1.0941e+02, 1.0821e+03, 3.5620e-06, 2.3835e-02, 2.8733e-02, 1.1356e+00])

我们还可以通过减去平均值并除以标准差来对数据进行归一化，这有助于我们的学习过程

data_normalized = (data - data_mean) / torch.sqrt(data_var)
print(data_normalized)

输出
tensor([[-1.7304, -0.5282,  0.3473,  ...,  0.4462, -0.9330, -1.3353],
        [-1.7283, -0.2985,  1.9668,  ..., -0.7197,  0.1289, -0.5846],
        [-1.7261, -0.2985,  1.2967,  ..., -0.3311, -0.0481, -0.5846],
        ...,
        [ 1.7261, -1.1600, -0.0995,  ...,  0.7053,  0.5419,  0.5415],
        [ 1.7283, -1.3897,  0.6544,  ...,  1.6769,  0.3059, -0.2092],
        [ 1.7304, -1.3323, -1.2165,  ...,  0.5110,  0.0109,  0.5415]])
        
标准化处理的主要作用包括：

1. 使不同量纲的特征具有可比性，消除量纲影响
2. 加速梯度下降的收敛
3. 提高模型的数值稳定性
4. 使特征对模型的贡献更加均衡
5. 有助于正则化，防止某些特征因为数值较大而主导模型

寻找阈值

接下来，让我们分析数据，看看是否有一种简单的方法可以快速分辨出好酒和劣质酒，首先，我们要确定target中哪些行对应的分数小于或者等于3

bad_indexes = target <= 3
#前面提到target是复制所有行和最后一列，检测哪一行对应分数小于3
print(bad_indexes.shape, bad_indexes.dtype, bad_indexes.sum())

输出
torch.Size([1599]) torch.bool tensor(10)

只有10个bad_indexs记录项被设置为True，通过使用pytorch中高级索引的功能，我们可以使用数据类型torch.bool来索引张量data，这实际上是在过滤张量data，使其仅仅包含索引张量中与True对应的项或者行，张量bad_ubdexs与张量target具有相同的形状，其值为True或者是False取决于我们的阈值与原始张量target的比较结果

bad_data = data[bad_indexes]
#索引出data中哪些行分数小于3，高级索引功能
print(bad_data.shape)

输出
torch.Size([10, 12])

新的张量bad_data有10行，与张量bad_indexes中true的函数相等，它保留了所有列，现在开始我们可以把葡萄酒分为好酒，中等酒和劣质酒3类，让我们对每一行使用mean()函数

实现了根据红酒质量评分将数据分组，并计算各组特征的平均值，最后以格式化方式打印比较结果
#数据分组
bad_data = data[target <= 3]
mid_data = data[(target > 3) & (target < 7)]
good_data = data[target >= 7]
#计算各组平均值
bad_mean = torch.mean(bad_data, dim=0)
mid_mean = torch.mean(mid_data, dim=0)
good_mean = torch.mean(good_data, dim=0)
- 对每组数据沿着维度0（行维度）计算平均值
- 结果是三个一维张量，每个张量包含对应组别中每个特征的平均值
- 这样可以比较不同质量红酒在各个特征上的平均差异

for i,args in enumerate(zip(col_list,bad_mean,mid_mean,good_mean)):
    print('{:2} {:20} {:6.2f} {:6.2f} {:6.2f}'.format(i,*args))
- 使用 zip 函数将特征名称（ col_list ）和三组平均值合并为元组序列
- enumerate 添加了索引计数
- 格式化打印每个特征的信息：
- {:2} ：索引号，占2个字符位置
- {:20} ：特征名称，占20个字符位置
- {:6.2f} ：平均值，占6个字符位置，保留2位小数
- *args 将元组解包为多个参数传入 format 方法
    
 输出
 0                      1053.20 793.14 831.71
 1 fixed.acidity          8.36   8.24   8.85
 2 volatile.acidity       0.88   0.54   0.41
 3 citric.acid            0.17   0.26   0.38
 4 residual.sugar         2.63   2.51   2.71
 5 chlorides              0.12   0.09   0.08
 6 free.sulfur.dioxide   11.00  16.21  13.98
 7 total.sulfur.dioxide  24.90  48.46  34.89
 8 density                1.00   1.00   1.00
 9 pH                     3.40   3.31   3.29
10 sulphates              0.57   0.65   0.74
11 alcohol                9.95  10.25  11.52

这里能发现一些问题，劣质葡萄酒的二氧化硫的含量似乎更高，我们可以使用二氧化硫的总量的阈值来作为区分好酒和劣质酒的粗略标准，让我们看看二氧化硫总量低于我们之前计算的平均值的索引

total_sulfur_threshold = 141.83
#设定了一个阈值值141.83，这个值用于判断红酒的总二氧化硫含量
total_sulfur_data = data[:,6]
#从数据集中提取第7列（索引为6）的数据，这一列代表红酒的总二氧化硫含量
predicted_indexes = torch.lt(total_sulfur_data,total_sulfur_threshold)
- 使用 torch.lt 函数（less than，小于）比较每个样本的总二氧化硫含量是否小于设定的阈值
- 返回一个布尔型张量，对于总二氧化硫含量小于141.83的样本，对应位置为 True ，否则为 False
print(predicted_indexes.shape, predicted_indexes.dtype,predicted_indexes.sum())

输出
torch.Size([1599]) torch.bool tensor(1599)

接下来，我们需要得到真正好酒的索引

actual_indexes = target > 5
print(actual_indexes.shape, actual_indexes.dtype,actual_indexes.sum())

输出
torch.Size([1599]) torch.bool tensor(855)

实际上的优质葡萄酒要比通过阈值测出的数量多，大概700瓶，现在我们看啊可能我们的预测和实际排名是否相符

n_matches = torch.sum(actual_indexes & predicted_indexes).item()
#进行逻辑与操作，找出同时满足两个条件的样本：实际质量好（评分>5）且预测为质量好（总二氧化硫<141.83）
n_predicted = torch.sum(predicted_indexes).item()
#计算模型预测为高质量的红酒样本总数
n_actual = torch.sum(actual_indexes).item()
#计算实际高质量（评分>5）的红酒样本总数

print(n_matches, n_matches / n_predicted, n_matches / n_actual)
#打印三个指标：
- 真正例数量
- 精确率（Precision）：正确预测为高质量的样本占所有预测为高质量样本的比例
- 召回率（Recall）：正确预测为高质量的样本占所有实际高质量样本的比例
输出
855 0.5347091932457786 1.0

预测正确855瓶，53%概率可以预测一瓶酒是好酒，识别出了所有的好酒，这个模型确实是高质量的，得到我们所预期的了，但是这跟随机说实话差不了多少，实际情况葡萄酒的质量不只是有这些因素决定的

在后面的简单的神经网络就可以客服这些限制，就像许多其他的基本的机器学习的方法一样，后面也会之间构建自己的第一个神经网络